


Next: Diffusion coefficient
Up: Diffusion effects
Previous: Rate equations
Contents
As mentioned in the previous section each non-equivalent lattice site results into a Lorentzian line in the energy domain or a exponential function in the time domain, respectively. The relatively complicated mathematical formalism of rate equations becomes much more concise in the case of a Bravais lattice. The definition of the Bravais lattice, i.e. a lattice with only one non-equivalent lattice site in the primitive cell, makes it possible to define only one jump frequency 1/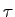 and the jump matrix A from equation
and the jump matrix A from equation ![[*]](crossref.png) reduces into a scalar. The line width
reduces into a scalar. The line width 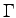 which is inserted into the frequency dependent refractive index (equation
which is inserted into the frequency dependent refractive index (equation ![[*]](crossref.png) ) is in the case of N different jump vectors
) is in the case of N different jump vectors 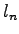
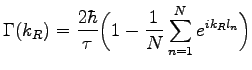 |
|
|
(73) |
Especially the b.c.c. structure, which is a Bravais structure, plays an important role in this work for the section about the Fe/MgO(001). There are eight nearest neighbours (NN) in this structure. Assuming an NN jump-diffusion mechanism eight jump vectors 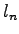 can be defined (the origin of the used system is the atom in the center of the cube in figure
can be defined (the origin of the used system is the atom in the center of the cube in figure ![[*]](crossref.png) ):
):
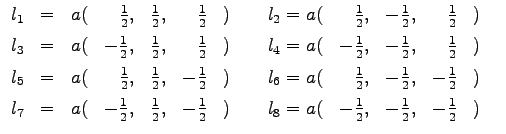 |
|
|
(74) |
Two jump vectors are shown in figure ![[*]](crossref.png) . Inserting this set into equation
. Inserting this set into equation ![[*]](crossref.png) the following simple formula for the line width
the following simple formula for the line width 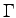 can be calculated
can be calculated
where 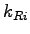 is the
is the 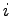 -th component of the reflected wave vector and
-th component of the reflected wave vector and 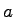 is the lattice constant of iron (
is the lattice constant of iron (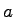 =2.86
=2.86 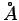 ) [44].
) [44].
Figure:
Simulated angular dependence of the line width for a nearest neighbour jump-diffusion mechanism sketched in the right part of the figure. The angle 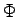 is the angle between the reflected wave vector k
is the angle between the reflected wave vector k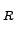 and the (010) axis of the b.c.c.structure.
and the (010) axis of the b.c.c.structure.
![\includegraphics[width=\textwidth]{pics/bcc_linewidth}](img289.png) |



Next: Diffusion coefficient
Up: Diffusion effects
Previous: Rate equations
Contents
Marcel Sladecek
2005-03-22
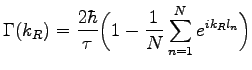
![[*]](crossref.png) reduces into a scalar. The line width
reduces into a scalar. The line width ![[*]](crossref.png) ) is in the case of N different jump vectors
) is in the case of N different jump vectors ![]() can be defined (the origin of the used system is the atom in the center of the cube in figure
can be defined (the origin of the used system is the atom in the center of the cube in figure ![[*]](crossref.png) ):
):
![[*]](crossref.png) . Inserting this set into equation
. Inserting this set into equation ![[*]](crossref.png) the following simple formula for the line width
the following simple formula for the line width ![]() can be calculated
can be calculated
![]() is the
is the ![]() -th component of the reflected wave vector and
-th component of the reflected wave vector and ![]() is the lattice constant of iron (
is the lattice constant of iron (![]() =2.86
=2.86 ![]() ) [44].
) [44].
![\includegraphics[width=\textwidth]{pics/bcc_linewidth}](img289.png)