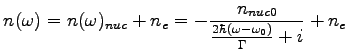 |
(37) |
![[*]](crossref.png) ), the refractive index reflects all of the resonances of the investigated medium. This statement immediately implies the energetic dependency of the refractive index. The refractive index can be split into the frequency dependent or nuclear part (
), the refractive index reflects all of the resonances of the investigated medium. This statement immediately implies the energetic dependency of the refractive index. The refractive index can be split into the frequency dependent or nuclear part (![[*]](crossref.png) which is, within the line width of the resonance, assumed to be constant. The nuclear part of the complex refractive index reflects the Mössbauer resonance in the medium and has a complex Lorentzian line shape [30,31]
which is, within the line width of the resonance, assumed to be constant. The nuclear part of the complex refractive index reflects the Mössbauer resonance in the medium and has a complex Lorentzian line shape [30,31]
The real and imaginary parts of the refractive index for the 14.4 ![]() resonance in
resonance in ![]() Fe are shown in figure
Fe are shown in figure ![[*]](crossref.png) as a function of energy in natural line width units.
as a function of energy in natural line width units.
![[*]](crossref.png) as
as
![\includegraphics[width=0.8\textwidth]{pics/e_profile}](img181.png)
|
The transmitted wave ![]() is at the resonance position in phase with the initial wave, since the real part of the refractive index is zero and is strongly damped due to the imaginary part of the refractive index which has an extremal value (see figure
is at the resonance position in phase with the initial wave, since the real part of the refractive index is zero and is strongly damped due to the imaginary part of the refractive index which has an extremal value (see figure ![[*]](crossref.png) ). Far from resonance the attenuation is low but the wave has a large phase shift.
). Far from resonance the attenuation is low but the wave has a large phase shift.
The factor ![]() has the character of an effective thickness known from conventional Mössbauer spectroscopy. Large effective thickness will broaden and enhance the energy profile of the transmitted wave (equation
has the character of an effective thickness known from conventional Mössbauer spectroscopy. Large effective thickness will broaden and enhance the energy profile of the transmitted wave (equation ![[*]](crossref.png) ) and multiple scattering effects cause a ``double hump structure'' shown in figure
) and multiple scattering effects cause a ``double hump structure'' shown in figure ![[*]](crossref.png) for three different values of the effective thickness. Since in NRS the response of the nuclei is measured as a function of time after excitation the time dependence of a transmitted field is the Fourier transformation of the energy profile. Two parts of the ``double hump structure'' at different but very similar energies interfere and cause beats in the time spectrum. These beats are called dynamical beats.
for three different values of the effective thickness. Since in NRS the response of the nuclei is measured as a function of time after excitation the time dependence of a transmitted field is the Fourier transformation of the energy profile. Two parts of the ``double hump structure'' at different but very similar energies interfere and cause beats in the time spectrum. These beats are called dynamical beats.
This refractive index formalism is analogous to the usually chosen approach when the universal scattering function
![]() , obtained by a Laplace transformation of the intermediate-scattering function [28], is used to calculate the time spectra. The refractive index reflects all dynamical effects in the sample for NRS, QMS and QNS scattering experiments. The formalism of the energy dependent refraction index was chosen in this work to emphasise the analogy to the electronic scattering part in the previous chapter.
, obtained by a Laplace transformation of the intermediate-scattering function [28], is used to calculate the time spectra. The refractive index reflects all dynamical effects in the sample for NRS, QMS and QNS scattering experiments. The formalism of the energy dependent refraction index was chosen in this work to emphasise the analogy to the electronic scattering part in the previous chapter.