


Next: Reflectivity from a homogeneous
Up: Snellīs law and Fresnel
Previous: The refractive index and
Contents
In the previous section the absorption (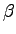 ) was neglected in the estimation of the value of the critical angle. For the further calculation of the transmission and reflectivity it is necessary to take this effect into account. The starting point is again the Snell's law (eq.
) was neglected in the estimation of the value of the critical angle. For the further calculation of the transmission and reflectivity it is necessary to take this effect into account. The starting point is again the Snell's law (eq. ![[*]](crossref.png) ). The cosines can be expanded again corresponding to equation
). The cosines can be expanded again corresponding to equation ![[*]](crossref.png) and Snell's law can be written as
and Snell's law can be written as
 |
(15) |
or using equation ![[*]](crossref.png) as
as
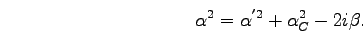 |
(16) |
The incident (I), reflecting (R) and transmitted (T) X-ray radiation can be treated as plane waves as sketched in the figure ![[*]](crossref.png)
The Fresnel equations, i.e. the reflectivity 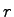 and the transmission
and the transmission 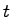 can be written using the definitions of
can be written using the definitions of 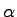 and
and 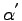 and the continuous conditions in a very simple way
and the continuous conditions in a very simple way
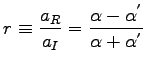 |
|
|
|
| |
|
|
(18) |
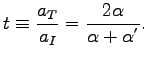 |
|
|
|
| |
|
|
|
From figure ![[*]](crossref.png) and equation
and equation ![[*]](crossref.png) it is clear that the transmitted wave is damped with increasing depth.
it is clear that the transmitted wave is damped with increasing depth.
The amplitude is
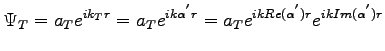 |
|
|
(19) |
| |
|
|
|
This exponential behaviour defines the penetration depth 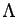 at which the intensity falls to the
at which the intensity falls to the 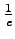 of the initial value
of the initial value
 |
(20) |
The region which is investigated during a grazing incidence experiment is first of all defined by the incident angle. An other important parameter is the angle between the refracted beam and the surface (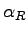 ) in the case of coplanar but asymmetric scattering. The region from which the information is received is smaller when decreasing this angle. In this way an information depth
) in the case of coplanar but asymmetric scattering. The region from which the information is received is smaller when decreasing this angle. In this way an information depth 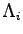 which is a combination of the known penetration depth
which is a combination of the known penetration depth
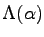 (equation
(equation ![[*]](crossref.png) ) and its analogon
) and its analogon
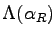 where
where
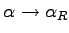 is reached (similar to the definition of the penetration depth in [22]).
is reached (similar to the definition of the penetration depth in [22]).
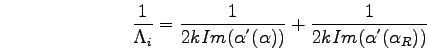 |
(21) |
The amplitude of the reflectivity 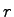 is strongly dependent on the incident angle
is strongly dependent on the incident angle 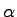 . The angular area can be divided into two characteristic regions separated by the critical angle.
. The angular area can be divided into two characteristic regions separated by the critical angle.
The first is the region below the critical angle. In this region 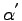 is almost imaginary. It means the transmitted wave is very strong damped and the penetration depth is more or less independent from the incident angle
is almost imaginary. It means the transmitted wave is very strong damped and the penetration depth is more or less independent from the incident angle 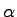 . It is typically in the range of a few 10
. It is typically in the range of a few 10
 in this region. The transmitted wave propagates along the surface in this small region defined by the penetration depth--it is called
in this region. The transmitted wave propagates along the surface in this small region defined by the penetration depth--it is called  wave.
wave.
In the second region, above the critical angle, the amplitude of the reflectivity decays with
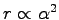 and the intensity
and the intensity
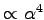 . This fast decay (
. This fast decay (
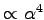 ) of the intensity is the reason for troubles during experiments, especially if one is interested in higher wave vector transfers (very small thicknesses, small correlation lengths,...).
) of the intensity is the reason for troubles during experiments, especially if one is interested in higher wave vector transfers (very small thicknesses, small correlation lengths,...).
The critical angle is the point where the reflectivity 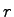 is almost 1. The reflected wave is in phase with the incident wave. The interference of both waves results into the maximum (fig.
is almost 1. The reflected wave is in phase with the incident wave. The interference of both waves results into the maximum (fig. ![[*]](crossref.png) ) of the
) of the  wave propagating along the surface. The penetration depth is at this position
wave propagating along the surface. The penetration depth is at this position
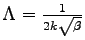 as can be calculated from equations
as can be calculated from equations ![[*]](crossref.png) and
and ![[*]](crossref.png) (
(
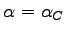 ). Typical values of penetration depths for the 14.4
). Typical values of penetration depths for the 14.4 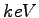 radiation in metals are in the order of a few hundred
radiation in metals are in the order of a few hundred
 . The angular behaviour of the reflectivity, transmission, the phase between the incident and reflected wave and the penetration depth is in more detail shown in figure
. The angular behaviour of the reflectivity, transmission, the phase between the incident and reflected wave and the penetration depth is in more detail shown in figure ![[*]](crossref.png) .
.
Figure:
Summary of the angular behaviour of the Fresnel reflectivity, the penetration depth, transmission and the phase between the incident and reflected wave for different values of the normalised absorption
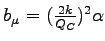 .
.
![\includegraphics[width=\textwidth]{pics/summary_reflectivity}](img88.png) |
As described in the previous paragraph the critical angle divides the angular region into two very different areas. Due to this the angles are usually normalised to the critical angle. For diffraction experiments it seems to be more useful to normalise the angles relative to wave vector transfers. In the case of a radiation with a wave vector 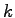 and the incident angle
and the incident angle 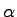 the corresponding wave vector transfer
the corresponding wave vector transfer 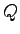 describing a elastic scattering scattering process is
describing a elastic scattering scattering process is
 |
(22) |
The normalisation to the wave vector transfer at the critical angle leads immediately to the definition of a dimensionless wave vector transfer
This definition allows to rewrite the equations ![[*]](crossref.png) into
into
These equations describe the reflectivity 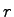 and transmission
and transmission 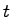 of an infinite thick layer. The possibility of a ``back'' reflection of the transmitted wave (T) which could interfere with the wave reflected at the surface (R) was not considered. In most cases the sample is a layer or multilayer on a substrate and the reflection at an additional interface substrate/layer has a drastic influence on the shape of the reflectivity. This case is discussed in the next section.
of an infinite thick layer. The possibility of a ``back'' reflection of the transmitted wave (T) which could interfere with the wave reflected at the surface (R) was not considered. In most cases the sample is a layer or multilayer on a substrate and the reflection at an additional interface substrate/layer has a drastic influence on the shape of the reflectivity. This case is discussed in the next section.



Next: Reflectivity from a homogeneous
Up: Snellīs law and Fresnel
Previous: The refractive index and
Contents
Marcel Sladecek
2005-03-22
![[*]](crossref.png) ). The cosines can be expanded again corresponding to equation
). The cosines can be expanded again corresponding to equation ![[*]](crossref.png) and Snell's law can be written as
and Snell's law can be written as
![[*]](crossref.png) as
as
![[*]](crossref.png)
![]() and the transmission
and the transmission ![]() can be written using the definitions of
can be written using the definitions of ![]() and
and ![]() and the continuous conditions in a very simple way
and the continuous conditions in a very simple way
![[*]](crossref.png) and equation
and equation ![[*]](crossref.png) it is clear that the transmitted wave is damped with increasing depth.
it is clear that the transmitted wave is damped with increasing depth.
![[*]](crossref.png) ) and its analogon
) and its analogon
![[*]](crossref.png) ) of the
) of the ![[*]](crossref.png) and
and ![[*]](crossref.png) (
(
![[*]](crossref.png) .
.
![\includegraphics[width=\textwidth]{pics/summary_reflectivity}](img88.png)
![]() and the incident angle
and the incident angle ![]() the corresponding wave vector transfer
the corresponding wave vector transfer ![]() describing a elastic scattering scattering process is
describing a elastic scattering scattering process is
![[*]](crossref.png) into
into