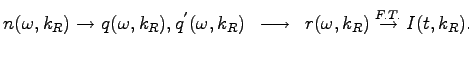 |
(54) |
![[*]](crossref.png) (Fresnel equations), the energy dependence of the refractive index was omitted. Indeed this is the most important point for the nuclear resonant scattering. Once defining the energy dependence, the calculation from the refractive index to the time spectrum measured during an NRS experiment follows a analogous way to the electronic reflectivity using an additional Fourier transform from energy to time domain
(Fresnel equations), the energy dependence of the refractive index was omitted. Indeed this is the most important point for the nuclear resonant scattering. Once defining the energy dependence, the calculation from the refractive index to the time spectrum measured during an NRS experiment follows a analogous way to the electronic reflectivity using an additional Fourier transform from energy to time domain
Carefully looking at the "recipe" ![[*]](crossref.png) one will recognise some kind of angular dependence of the refractive index introduced by k
one will recognise some kind of angular dependence of the refractive index introduced by k![]() . This seems to be in contradiction to the statement in section 2.4 about the validity of the reflectivity calculations for crystalline, polycrystalline and amorphous layers and the equations
. This seems to be in contradiction to the statement in section 2.4 about the validity of the reflectivity calculations for crystalline, polycrystalline and amorphous layers and the equations ![[*]](crossref.png) and
and ![[*]](crossref.png) where no angular dependence is explicitly written. The angular dependence introduced here will be explained in detail in the Chapter
where no angular dependence is explicitly written. The angular dependence introduced here will be explained in detail in the Chapter ![[*]](crossref.png) and reflects the angular dependence of the accelerated decay of the delayed intensity.
and reflects the angular dependence of the accelerated decay of the delayed intensity.
Using the frequency dependent refractive index from equation ![[*]](crossref.png) the dimensionless wave vector transfers
the dimensionless wave vector transfers ![]() and
and ![]() and finally the reflectivity
and finally the reflectivity ![]() can be calculated in analogy to equations
can be calculated in analogy to equations ![[*]](crossref.png) and
and ![[*]](crossref.png) .
.
The result is a reflectivity which is a function of the incident and exit angle (![]() and
and ![]() ) and of the frequency. A typical NRS experiment is performed in a fixed geometry, i.e. for
) and of the frequency. A typical NRS experiment is performed in a fixed geometry, i.e. for ![]() =const. and
=const. and ![]() =const., and the time response of the sample is measured. A detailed description of the experimental setup and the measurement procedure can be found in Chapter
=const., and the time response of the sample is measured. A detailed description of the experimental setup and the measurement procedure can be found in Chapter ![[*]](crossref.png) . According to equation
. According to equation ![[*]](crossref.png) the last step on the way to calculate the measured intensity (delayed intensity) is the Fourier transform in time of the reflectivity
the last step on the way to calculate the measured intensity (delayed intensity) is the Fourier transform in time of the reflectivity ![]() (equation
(equation ![[*]](crossref.png) ). This seems to be clear since the lifetime of the used nuclear transition is connected with the line width of the used resonance with a Heisenberg uncertainty relation. One would expect that in the simplest case (no multiple scattering, unsplit resonance) the shape of the time spectrum is a simple exponential with a decay corresponding to the lifetime of the transition of the Mössbauer nucleus.
). This seems to be clear since the lifetime of the used nuclear transition is connected with the line width of the used resonance with a Heisenberg uncertainty relation. One would expect that in the simplest case (no multiple scattering, unsplit resonance) the shape of the time spectrum is a simple exponential with a decay corresponding to the lifetime of the transition of the Mössbauer nucleus.
The calculation of a time response of a multilayer sample is very similar. The only difference is the necessity to calculate the total reflectivity ![]() of the multilayer using Parratt's exact recursive method (equation
of the multilayer using Parratt's exact recursive method (equation ![[*]](crossref.png) ) and the proper parameters for the N
) and the proper parameters for the N![]() layer.
layer.